Chapter - 8 Motion

Yes, zero displacement is possible if an object has moved through a distance. Suppose a body is moving in a circular path and starts moving from point A and it returns back at same point A after completing one revolution, then the distance will be equal to its circumference while displacement will be zero.

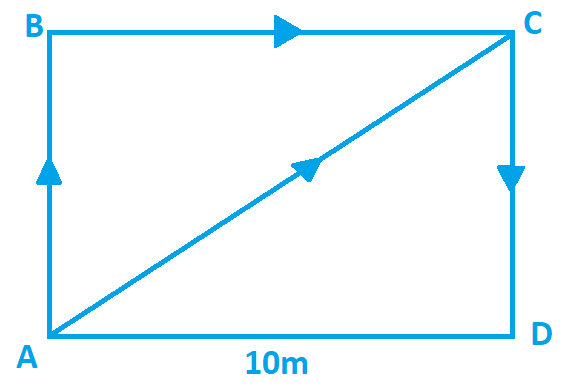
Given, side of the square field = 10 m
Therefore, perimeter = 10 m × 4 = 40 m
Farmer moves along the boundary in 40 s
Time = 2 minutes 20 s = 2 × 60 s + 20 s = 140 s
since, in 40 s farmer moves 40 m
Therefore, in 1s distance covered by farmer = 40 ÷ 40 = 1m.
Therefore, in 140s distance covered by farmer = 1 × 140 m = 140 m
Now, number of rotation to cover 140 along the boundary =$\frac{Total dis\tan ce}{Perimeter}$

= 140 m ÷ 40 m = 3.5 round

Thus after 3.5 round farmer will at point C (diagonally opposite to his initial position) of the field.
Therefore, Displacement AC = $\sqrt{{10}^2}+ {10}^2$ = √200 = 10√2 m
Thus, after 2 minute 20 second the displacement of farmer will be equal to 10√2 m north east from initial position.

None of (a) and (b) are true.

Speed has only magnitude while velocity has both magnitude and direction. So speed is a scalar quantity but velocity is a vector quantity.

The magnitude of average velocity of an object will be equal to its average speed in the condition of uniform velocity in a straight line motion.

In automobiles, odometer is used to measure the distance.

In the case of uniform motion, the path of an object will look like a straight line.

Here we have, speed = 3×10⁸ m/s
Time = 5 minute = 5 × 60 s = 300 s
Using, Distance = Speed × Time
⇒ Distance = 3 ×10⁸ × 300 m = 900 × 10⁸ m= 9.0 × 10¹⁰ m

1. A body is said in uniform acceleration when its motion is along a straight line and its velocity changes by equal magnitude in equal interval of time.
2. A body is said in non-uniform acceleration when its motion is along a straight line and its velocity changes by unequal magnitude in equal interval of time.

Here we have,

u = 80 km/h = $\frac{80 \times 1000}{3600}$ms^-1 = $\frac{200}{9}$ms^-1

v = 60 km/h = $\frac{60 \times 1000}{3600}$ms^{-1 = $\frac{150}{9}$ms-1}

t = 5 s
Therefore, acceleration, a = ?
We know that, v = u + at

⇒ a = $\frac{v -u}{t}$

= $\frac{\left({\displaystyle \frac{150}{9}} - {\displaystyle \frac{200}{9}}\right)}{5}=\frac{{\displaystyle \frac{-50}{9}}}{5}=\frac{-10}{9}$

= -1.1 ms^-2

Therefore, Acceleration is -1.1 ms^-2

Here we have,

Initial velocity, u = 0 m/s

Final velocity, v = 40 km/h = $\frac{40\times 1000}{3600}$ms^-1  = $\frac{100}{9}$ms^-1

Time (t) = 10 minute = 60 × 10 = 600 s

Acceleration (a) =?

We know that, v = u + at

⇒ a = $\frac{v - u}{t}$ = $\frac{\left({\displaystyle \frac{100}{9}} - 0\right)}{600}$ = $\frac{1}{54}$ = 0.0185 ms⁻²

⇒ a = 0.0185 ms⁻²

• The slope of the distance-time graph for an object in uniform motion is straight line.
• The slope of the distance-time graph for an object in non-uniform motion is not a straight line.

When the slope of distance-time graph is a straight line parallel to time axis, the object is stationary.

When the graph of a speed time graph is a straight line parallel to the time axis, the object is moving with constant speed.

The quantity of distance is measured by the area occupied below the velocity time graph.

Here we have,
Initial velocity (u) = 0 m/s
Acceleration (a) = 0.1ms^–2
Time (t) = 2 minute = 120 seconds

(a) The speed acquired:
We know that, v = u + at
⇒ v = 0 + 0.1 × 120 m/s
⇒ v = 12 m/s
Thus, the bus will acquire a speed of 12 m/s after 2 minute with the given acceleration.

(b) The distance travelled:
We know that, s = ut + $\frac{1}{2}$at²
= 0 × 120 + $\frac{1}{2}$× 0.1 × (120)²
= $\frac{1}{2}$× 0.1 ×14400 m = 720 m

Thus, bus will travel a distance of 720 m in the given time of 2 minute.

Here, we have,
Initial velocity, u = 90 km/h = $\frac{90 \times 1000}{3600}$ ms^-1 = 25ms^-1

Final velocity, v = 0 m/s
Acceleration, a = – 0.5 m/s2
Distance travelled = ?

Using, v² = u² + 2as

s = $\frac{v^2 - u^2}{2a}$ = $\frac{0^2 -{25}^2}{2\left(-0.5\right)}$ = 625m

Therefore, train will go 625 m before it brought to rest.

Here we have,
Initial velocity, u = 0 m/s
Acceleration (a) = 2 cm/s² = 0.02 m/s²
Time (t) = 3 s
Final velocity, v = ?
We know that, v = u + at
Therefore, v = 0 + 0.02 × 3 m/s
⇒ v = 0.06 m/s
Therefore the final velocity of trolley will be 0.06 m/s after start.

Here we have,
Acceleration, a = 4 m/s²
Initial velocity, u = 0 m/s
Time, t = 10 s
Distance covered (s) =?
We know that, s = ut + $\frac{1}{2}$at²

⇒ s = 0 × 10 + $\frac{1}{2}$× 4 × (10)² m

⇒ s = 2 × 100 m
⇒ s = 200 m
Thus, racing car will cover a distance of 200 m after start in 10 s with given acceleration.

Here we have,
Initial velocity (u) = 5 m/s
Final velocity (v) = 0 m/s
Acceleration (a) = – 10 m/s²
Height, i.e. Distance, s =?
Time (t) taken to reach the height =?
We know that, v² = u² + 2as

⇒ 0 = (5)² + 2 × −10 × s

⇒ 0 = 25 − 20s
⇒ s = 25/20 m
⇒ s = 1.25 m

Now, we know that, v = u + at
⇒ 0 = 5 + (–10) × t
⇒ 0 = 5 − 10t
⇒ t = 5/10 s
⇒ t = 0.5 s
Thus, stone will attain a height of 1.25 m and time taken to attain the height is  0.5 s.

Time taken = 2 min 20 sec = 140 sec.
Radius, r = 100 m.
In 40 sec the athlete complete one round.
So, in 140 sec the athlete will complete = 140 ÷ 40 = 3.5 round.
⇒ Distance covered in 140 sec = 2πr × 3.5 = 2 × 22/7 × 100 × 3.5 = 2200 m.
At the end of his motion, the athlete will be in the diametrically opposite position.
⇒ Displacement = diameter = 200 m.

(a) For motion from A to B:
Distance covered = 300 m
Displacement = 300 m.
Time taken = 150 sec.
We know that, Average speed = Total distance covered ÷ Total time taken

= 300 m ÷ 150 sec = 2 ms^-1
Average velocity = Net displacement ÷ time taken
= 300 m ÷ 150 sec = 2 ms^-1

(b) For motion from A to C:
Distance covered = 300 + 100 = 400 m.
Displacement = AB - CB = 300 - 100 = 200 m.
Time taken = 2.5 min + 1 min = 3.5 min = 210 sec.
Therefore, Average speed = Total distance covered ÷ Total time taken

= 400 ÷ 210 = 1.90 ms^-1
.
Average velocity = Net displacement ÷ time taken
= 200 m ÷ 210 sec = 0.952ms^-1.

Let one side distance = x km.
Time taken for forward trip at a speed of 20 km/h = Distance / Speed = x/20 h.
Time taken in return trip at a speed of 30 km/h = x/30 h.
Total time for the whole trip = $\frac{x}{20} + \frac{x}{30} = \frac{3x + 2x}{60} = \frac{5x}{60}h$.

Total distance covered = 2x km.
We know, Average speed = Total distance ÷ Total time
= 2x ÷ (5x/60) = 24 kmh^-1

Here, u = 0 m/s
a = 3 ms-2
t = 8 s
Using, s = ut + 1⁄2 at²
s = 0 × 8 + 1⁄2 × 3 × 8² = 96 m.

In in the following graph, AB and CD are the time graphs for the two cars whose initial speeds are 52 km/h(14.4 m/s) and 34 km/h(8.9 m/s), respectively.

Distance covered by the first car before coming to rest
= Area of triangle AOB
= 1⁄2 × AO × BO
= 1⁄2 × 52 kmh^-1 × 5 s
= 1⁄2 x (52 × 1000 × 1/3600) ms^-1 × 5 s = 36.1 m
Distance covered by the second car before coming to rest
= Area of triangle COD
= 1⁄2 × CO × DO
= 1⁄2 × 34 km h^-1 × 10 s
= 1⁄2 × (34 × 1000 × 1/3600) ms^-1 ×10 s = 47.2 m
Thus, the second car travels farther than the first car after they applied the brakes.

1. B is travelling fastest as it is taking less time to cover more distance.
2. All three are never at the same point on the road as three lines do not cross at any common point.
3. Approximately 6 kms. [as 8 – 2 = 6]
4. Approximately 7 kms. [as 7 – 0 = 7]

Here, u = 0 m/s, s = 20 m, a = 10 ms^-2, v = ?, t = ?

Using v² – u² = 2as

We have, v² – 0² = 2 × 10 × 20 = 400 ⇒ v = 20 ms^-1.

and t = (v – u) ÷ a = 20 ÷ 10 = 2 s.

(a) Distance covered = area under speed – time

⇒ Distnce = $\frac{1}{2}$× 4 × 6 = 12 m
Shaded area representing the distance travelled is as follows:

(b) After 6 seconds the car moves in uniform motion (at a speed of 6 m/s).

(a) Yes, a body can have acceleration even when its velocity is zero. When a body is thrown up, at highest point its velocity is zero but it has acceleration equal to acceleration due to gravity.

(b) Yes, an acceleration moving horizontally is acted upon by acceleration due to gravity that acts vertically downwards.

Here,
r = 42250 km = 42250000 m
T = 24 h = 24 × 60 × 60 s
Using Speed, v = 2πr ÷ T
v = (2 × 3.14 × 42250000) ÷ (24 × 60 × 60) m/s
= 3070.9 m/s = 3.07 km/s